Practical example: Hyper-systolic routing algorithms
This article discusses communication routing strategies for data on massively parallel systems and supercomputers. Optimizations like this one can save thousands of dollars in real-world projects. This article is based on my talk published in the Proceedings of the International Conference ParCo 2001, pp. 370.
Table of contents:
The challenge
In many engineering and science applications one needs to compute mutual interactions between elements. One example is the force between bodies in molecular dynamics as they occur in astrophysics, thermodynamics and plasma physics. Other examples are polymer chains with long-range interactions, genome analysis, signal processing and statistical analysis of time series.
As each element interacts with every other element the computational effort grows with the power of two, i.e. n2 for n elements. For large numbers of elements – where large means substantially larger than the number of computing nodes – and complicated interactions the problem is computation-bound. However, when larger numbers of computing nodes are involved, the importance of communication grows substantially.
Similar to the article on data distribution we first sketch a simple scenario that has all features we are interested in. We start with eight compute nodes and eight data packets. Every node initially has one data packet and needs to perform a computation that involves “his” packet and all other packets.
| Node 1 | Node 2 | Node 3 | Node 4 | Node 5 | Node 6 | Node 7 | Node 8 |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
In the following we discuss how the nodes can communicate the data and why this is important.
Strategies of data routing
There are three strategies that solve the problem. Although their results agree, their efficiencies do not.
- Replicated data.
- All eight data packets are broadcast to all eight nodes who then proceed with their part of the calculation. This is the easiest but least efficient method.
- Systolic array.
- The process is split into seven steps. At each step one data packet is shifted, i.e., each node sends its own packet to the right and receives the neighbor's packet from the left. This method requires less space than the replicated data method. It is not faster.
- Hyper-systolic array.
- This method introduces an optimization by decreasing the communication at the expense of increased memory consumption.
To illustrate the key idea of hyper-systolic routing we first illustrate what the systolic routing looks like and then see how it can be improved.
Systolic array
As pointed out above, this method requires seven shifts of the data, each time communicating with next-neighbors. The packets travel as follows:
| Step | Node 1 | Node 2 | Node 3 | Node 4 | Node 5 | Node 6 | Node 7 | Node 8 |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 8 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 7 | 8 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 | 6 | 7 | 8 | 1 | 2 | 3 | 4 | 5 |
| 4 | 5 | 6 | 7 | 8 | 1 | 2 | 3 | 4 |
| 5 | 4 | 5 | 6 | 7 | 8 | 1 | 2 | 3 |
| 6 | 3 | 4 | 5 | 6 | 7 | 8 | 1 | 2 |
| 7 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 1 |
But we can do much better!
Hyper-systolic array
When looking at the communication table of the systolic array we notice a redundancy on the nodes: the pairing of data packets (1,4) for example occurs on node No. 5 at step 4, but still on all other nodes later on during the computation. There is no need to have data packet No. 4 shifted to node No. 1 in step 5 since the combination has already been available at step number 4. So instead of shifting packet number 4 to node 1 at step 5 the necessary computation could have been done by node number 5 with all information it already had available at step number 4.
But what about node number 1 during this time? Well, during the time node number 5 was busy with packets (1,4) node number 1 could have worked on packets (8,5) — which would otherwise get done at step number 5 by node number 5 in the systolic scheme.
This is the basic idea of hyper-systolic routing: Work more and talk less!
We still need to do the same number of computations as before, but we only need to communicate the information such that each combination of data packets occurs at least once. With a little experimenting we can find one possibility for eight nodes:
| Step | Node 1 | Node 2 | Node 3 | Node 4 | Node 5 | Node 6 | Node 7 | Node 8 |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 8 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 7 | 8 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 | 6 | 7 | 8 | 1 | 2 | 3 | 4 | 5 |
| 4 | 5 | 6 | 7 | 8 | 1 | 2 | 3 | 4 |
| 5 | 4 | 5 | 6 | 7 | 8 | 1 | 2 | 3 |
| 6 | 3 | 4 | 5 | 6 | 7 | 8 | 1 | 2 |
| 7 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 1 |
Thus, only three steps are needed, less than half of the original systolic array method. Admittedly, the resulting algorithm is more complex; the data is accumulated at different nodes and will need to get shifted back and summed up to yield the correct result. But the benefit turns out to become tremendous for larger numbers of nodes.
With a little more combinatorial arithmetics we can find general solutions to these communication patterns, see the proceedings contribution quoted at the beginning of this article. There can be more than one solutions, but the minimum number grows as the square root of the number of nodes. For a huge parallel computer with thousands of nodes we are talking about a reduction of factors of hundreds in communication!
Performance improvement
We have tested the result on the Wuppertal Alpha-Linux-Cluster-Engine (ALiCE) which at that time was a state-of-the-art cluster. Although back then it had only 128 nodes, we could observe a notable improvement in overall performance. The run-times are shown for a 64-node partition comparing the systolic and hyper-systolic arrays:
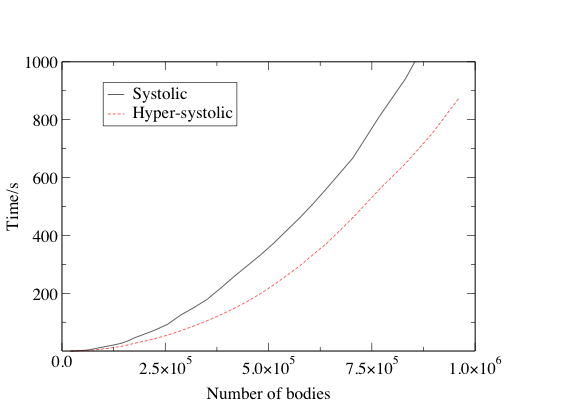
It is apparent that in reality the hyper-systolic algorithm is indeed faster than the systolic one and the benefit translates to thousands of dollars when the cost of the hardware is taken into account.
Conclusion
Hyper-systolic routing is a more complicated communication pattern and also not as easy to implement as the other schemes. On the other hand, even for machines with moderate numbers of nodes such as 64 the improvement turns out to be notable. For the fastest machines in use today – with thousands of nodes – the improvement is tremendous. Since parallel computers may cost millions of dollars such an optimization saves thousands of dollars.
Field-theory.org by NuAS / Dr. Wolfram Schroers is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.Additional permissions available at http://www.field-theory.org/editorial/index.html.